On this page

基本可行解

线性规划的约束条件定义了可行区域。如下图所示，可行区域是连续的，其中可行解有无穷多个。那么最优解适否存在。如果存在，如何找到它呢。因此，有必要研究一下最优解的性质。

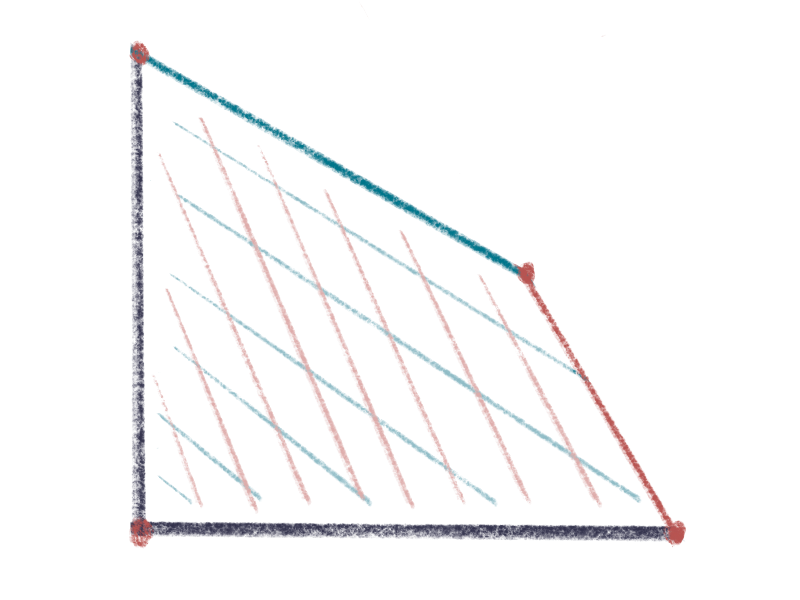
可以证明如下结论。

info

定理最优解是可行区域的一个顶点。

注意，顶点的数量是有限的。这样一来，最优解一定存在。可以枚举所有顶点，找到目标函数值最优的顶点。当然，枚举的效率太低，需要设计更好的算法。

但是，有一个概念没讲清楚。那就是，什么是顶点。从几何视角来看，顶点不难理解。接下里，需要从代数角度进行定义，这样才方便计算。

标准形

考虑线性规划的标准形式：

$$ \begin{aligned} \min~ & c^T x\\ \text{s.t.}~ & Ax=b\\ & x\geq 0 \end{aligned} $$

其中 $c, x \in \mathbb{R}^n$，$A\in\mathbb{R}^{m\times n}$，$b\in\mathbb{R}^m \geq \mathbf{0}$，$n\geq m$。

基矩阵

注意 $A$ 是一个 $m$ 行 $n$ 列的矩阵，可以把它看成 $n$ 个 $m$ 维的列向量。 $$ A = [a_1, a_2, …, a_n] $$ 其中 $a_j \in \mathbb{R}^m$，$j=1,2,…n$。

接下来把 $A$ 拆成两个部分： $$ A = [B \quad N] $$ 其中 $B$ 包含前 $m$ 列，因此 $B$ 是一个方阵，即 $B\in \mathbb{R}^{m\times m}$；而 $N$ 包含剩下的 $n-m$ 列，因此 $N \in \mathbb{R}^{m \times (n-m)}$。

假设 $A$ 是满秩矩阵，由于 $m\leq n$，那么它的秩是 $m$。考虑 $A$ 的列向量，它有一组基 (Basis)，即 $m$ 个线性无关的列向量。

如果 $B$ 不满秩，就把这组基换到前 $m$ 列，因此 $B$ 也是满秩的，或者说可逆的。我们称 $B$ 为基矩阵 (Basic Matrix)，称 $N$ 为非基矩阵 (Non-basic Matrix)。

基变量

相应地，把 $x$ 拆成两个部分，即

$$ x = \begin{bmatrix} x_B \\ x_N \end{bmatrix} $$

其中

$$ x_B = \begin{bmatrix} x_1 \\ \vdots\\ x_m \end{bmatrix}\quad x_N = \begin{bmatrix} x_{m+1} \\ \vdots\\ x_n \end{bmatrix} $$

把 $x_B$ 对应的变量称为基变量， $x_N$ 对应的变量称为非基变量。

例子

需要注意， $x_B$ 的下标与 $B$ 中的列一一对应。同理，$x_N$ 的下标与 $N$ 中的列一一对应。

举例说明。

$$ A = \begin{bmatrix} 1 & 0 & 0 & 4 & 0\\ 0 & 2 & 0 & 0 & 5\\ 0 & 0 & 3 & 0 & 0\\ \end{bmatrix}\quad x = \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_5 \end{bmatrix} $$

接下来划分 $B$ 和 $N$。

从 $A$ 的列中，任选三个线性无关的列作为 $B$。例如，选最后三列。

$$ B = \begin{bmatrix} 0 & 0 & 0\\ 0 & 4 & 5 \\ 3 & 0 & 0\\ \end{bmatrix} $$

那么 $N$ 就是剩下的两列。

$$ N = \begin{bmatrix} 1 & 0 \\ 0 & 2 \\ 0 & 0 \\ \end{bmatrix} $$

对应的 $x_B$ 和 $x_N$ 如下：

$$ x_B = \begin{bmatrix} x_3 \\ x_4\\ x_5 \end{bmatrix}\quad x_N = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} $$

基本解

考虑约束条件。把 $Ax=b$ 用分块矩阵来表示。

$$ \begin{aligned} A x & = [B \quad N] \begin{bmatrix} x_B\\ x_N \end{bmatrix}\\ & = Bx_B + N x_N\\ & = b \end{aligned} $$

即 $$ Bx_B + N x_N = b $$ 由于 $B$ 可逆，我们得到 $$ x_B = B^{-1}b - B^{-1}Nx_N $$

令 $x_N = \mathbf{0}$，那么 $x_B = B^{-1}b$，于是

$$ z:= \begin{bmatrix} x_B\\ x_N \end{bmatrix} = \begin{bmatrix} B^{-1}b\\ \mathbf{0} \end{bmatrix} $$

满足方程 $Az = b$。那么 $z$ 就称为基本解 (Basic Solution)。