从一个例子开始。

$$ \begin{aligned} \max~ & 5x_1 + 3x_2\\ \text{s.t. }& x_1 + 2x_2 \leq 8\\ & 3x_1 + 4x_2 \leq 20\\ & x_1\geq 0, x_2\geq 0 \end{aligned} $$

接下来看它的约束条件。

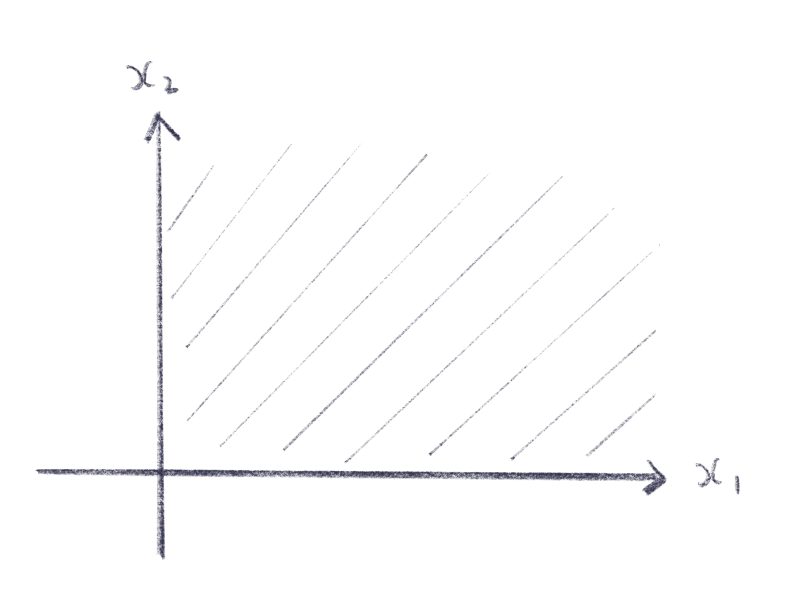
把 $x_1,x_2$ 看成平面的两条坐标轴，那么 $x_1\geq 0$ 和 $x_2\geq 0$ 就表示下面的区域。

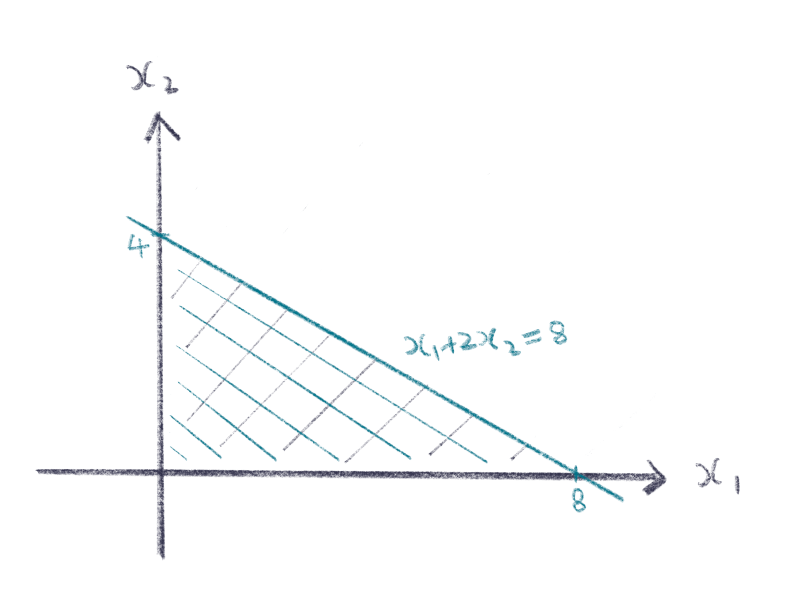
第一个不等式 $x_1 + 2x_2 \leq 8$，它表示直线 $x_1+2x_2=8$ 的下半边部分。把它跟 $x_1\geq 0$ 和 $x_2\geq 0$ 取交集，如下图所示。

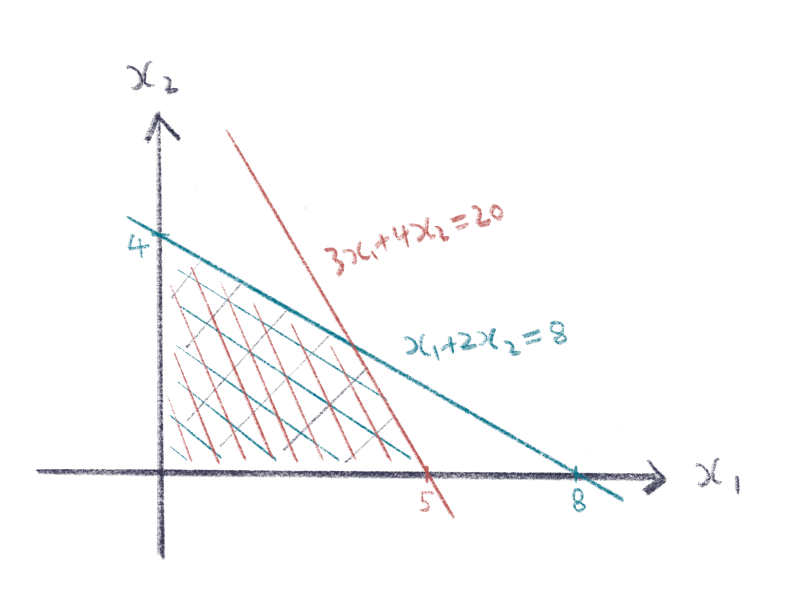
第二个约束条件 $3x_1 + 4x_2 \leq 20$，它表示直线 $3x_1 + 4x_2 \leq 20$ 的左半边部分。再把它跟前面的区域取交集。

可行域

所有约束条件取交集，得到的点 $x=(x_1,x_2)$ 的集合，称为可行区域 (Feasible Region)，或者叫可行域。

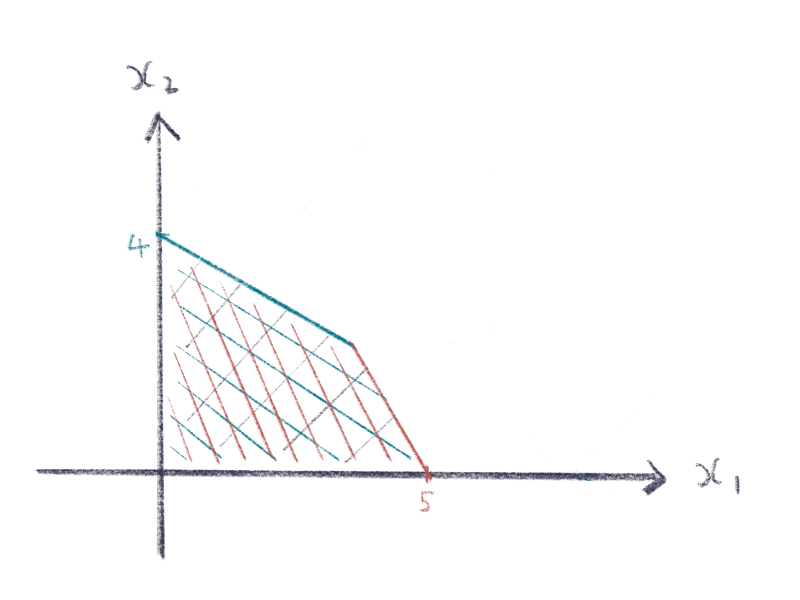
如果一个点 $x$ 在可行域中，就称为可行解 (Feasible Solution)；否则称为不可行解 (Infeasible Solution)。

多面体

接下来把上面的概念扩展到高维的情况。考虑线性规划问题的标准形式。

$$ \begin{aligned} \min~ & c^T x\\ \text{s.t.}~ & Ax=b\\ & x\geq 0 \end{aligned} $$

其中 $c, x \in \mathbb{R}^n$，$A\in\mathbb{R}^{m\times n}$，$b\in\mathbb{R}^m \geq \mathbf{0}$，$n\geq m$。

注意 $Ax=b$ 代表 $m$ 个等式约束，如下所示。

$$ \begin{aligned} & a_{11} x_1 + a_{12} x_2 + ... + x_{1n}x_n = b_1\\ & a_{21} x_1 + a_{12} x_2 + ... + x_{1n}x_n = b_1\\ & \quad \vdots \\ & a_{m1} x_1 + a_{m2} x_2 + ... + x_{1n}x_n = b_m\\ \end{aligned} $$

其中每一个等式可以看成一个超平面 (Hyperplane)，这些超平面的交集形成一个多面体 (Polyhedra)

$$ P = \{x| Ax=b, x\geq 0 \} $$

多胞形

如果一个多面体是有界的，就叫它多胞形 (Polytope)。

用例子解释一下。

考虑两个约束条件 $x_1\geq 0$，$x_2\geq 0$。定义点集 $P_1$ 如下。

$$ P_1 = \{(x_1,x_2) | x_1\geq 0 , x_2\geq0 \} $$

那么 $P_1$ 所示的区域就是这个样子。

这个区域不是有界的。换句话说，$x_1$ 或 $x_2$ 可以无限大。因此， $P_1$ 是一个多面体，但不是多胞形。

再看一个例子。

$$ \begin{aligned} P_2 = \{(x_1,x_2) ~|~ & x_1 + 2x_2 \leq 8, \\ & 3x_1 + 4x_2 \leq 20,\\ & x_1\geq 0 , x_2\geq0\}\\ \end{aligned} $$

它是下面这个样子。

它是有界的，因此它是多胞形。注意：多胞形也是多面体，它是有界的多面体。

Edit this page

Last updated 28 Mar 2025, 10:46 +0800 . history